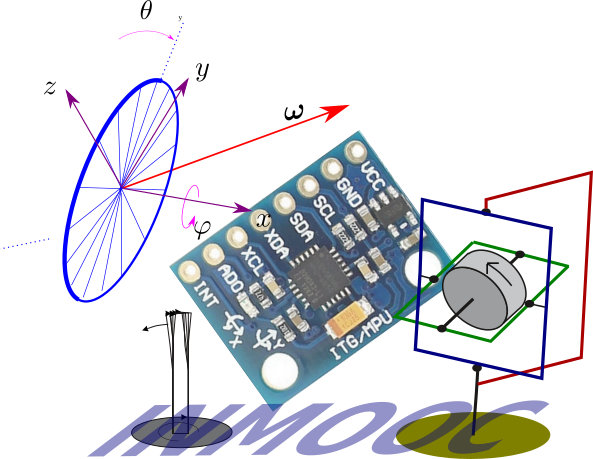
|
|
|
|
|
|
|
|
|
|
InMOOC is a free MOOC open to everybody. It corresponds more or less to chapter 1 of the book
"Mobile Robotics, Luc Jaulin (2015), ISTE editions".
This MOOC requires notions in mathematics
(typically those that are needed to enter engineering schools in France).
It is supposed to be in English, but some videos associated to exercises are still in French.
Inertial techniques are used in several topics of mobile robotics. They are used
- to deal with data coming from an inertial measurement unit (IMU) which is a device that measures
angular rates and accelerations to estimate a position of a robot
- for finding a dynamical model for a robot in a 3D environment with a position and orientation that may
change with respect to the different forces and torques.
- to compute the input to apply to the robot so that it will move toward the right direction
Inertial tools are used in different types of robots /vehicles such as autonomous aircraft, underwater robots, satellites, car, etc.
In this MOOC, you will learn who to:
- Build the sensors that are able to measure the angular rate and the accelerations of a body inside its own frame;
- Derive the state equations which a 3D robot controlled with accelerations or forces;
- Integrate these state equations using an integration algorithm (Runge-Kutta for instance);
- Characterize and control the integration errors
To register fill the form :
The registration is not mandatory to follow the MOOC and to see the videos.
But it is needed to have to get the diploma.
To follow InMOOC, you should have some basic notions in Python
and good knowledge in mathematics.
If you do not know Python, but any other programming language,
you may learn easily the required notions in this MOOC.
You will have to install Python 3 in your machine.
A video with explanations related to each exercise is given as soon as the lesson opens. You are not obliged to follow the method that is given in the video.
To get the diploma, you need at least 25 points.
Therefore, doing all exercises is not mandatory.
The participants who got enough points will receive a diploma corresponding this MOOC.
This diploma can be used by students to obtain the corresponding
ECTS
from their PhD courses, or to comply with any other requests by their home university.
If needed by your doctoral school, I can also provide a 20 minutes Skype exam with a mark, once the MOOC is finished.
An example of the diploma you can obtain :
For all questions, delays, etc
send an email to jaulin.inmooc@gmail.com
For each lesson, you should send your solution by email to jaulin.inmooc@gmail.com
For the exercises that require the execution of a program,
You should provide the Python (or other) code.
You should also send a pdf file with some explanations and screen captures of the running program.
For some exercises, the solution corresponds to text and equations and no program is required.
In such a case, you should post a scan of your paper sheet,
(taken with you phone for instance) or any pdf file.
pdf files for the lessons and the exercises.
Starting programs for Python users.
For Python users, use the library roblib.py.
For Python users, draw in 3D view3dlib.py.
