
This microsite is associated to the paper
![]()
![]() L. Jaulin (2023).
Inertial control of the a spinning flat disk
L. Jaulin (2023).
Inertial control of the a spinning flat disk
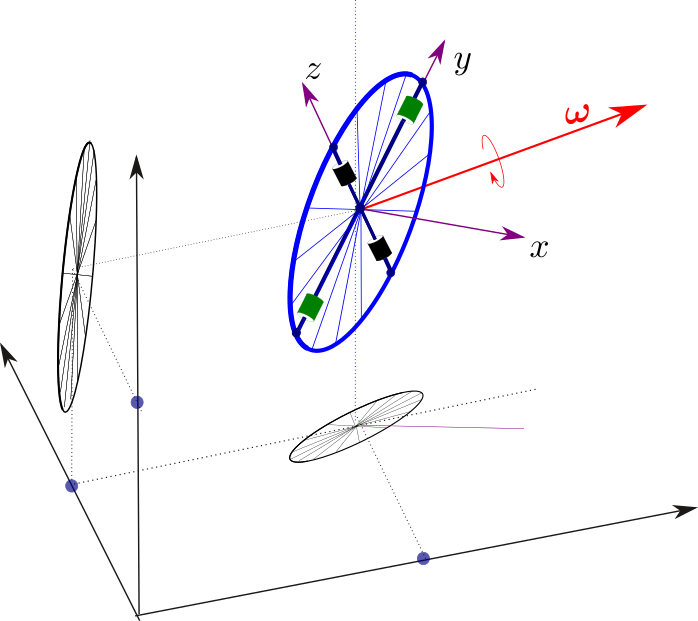
An illustration of the change of rotation without external forces :
![]()
from roblib import * # available at https://www.ensta-bretagne.fr/jaulin/roblib.py
def draw_wheel(R,I,wr,colorwheel="black"):
clean3D(ax,-3,3,-3,3,-1,5)
w=R@wr
L=R@I@wr # angular momentum
draw_arrow3D(ax,0,0,2,0.02*L[0,0],0.02*L[1,0],0.02*L[2,0],"red")
draw_arrow3D(ax,0,0,2,0.1*w[0,0],0.1*w[1,0],0.1*w[2,0],"green") # spin vector
l2,l3=sqrt(abs(I[2,2]-I30+0.5)),sqrt(abs((I[1,1]-I20+0.5)))
M=tran3H(0,0,2)@ToH(R)@wheel3H(r)
draw3H(ax,M,colorwheel,True,1)
def draw_masses(l2,l3,col):
p=array([[0],[0],[2]])+R@array([[0],[l2],[l3]])
ax.scatter(*p,color=col)
draw_masses(l2,0,'green')
draw_masses(-l2,0,'green')
draw_masses(0, l3,'black')
draw_masses(0,-l3,'black')
pause(0.001)
def f(x,u):
w1,w2,w3,I2,I3=x[0,0],x[1,0],x[2,0],x[3,0],x[4,0]
I1=I2+I3
u1,u2=u[0,0],u[1,0]
dw1=-((I3-I2)/I1)*w2*w3-w1*(u1+u2)/I1
dw2=-w3*w1-w2*u1/I2
dw3= w1*w2-w3*u2/I3
dI2=u1
dI3=u2
return array([[dw1],[dw2],[dw3],[dI2],[dI3]])
ax= Axes3D(figure())
dt=0.002
r=1
m=10
R=eye(3)
w=array([[10],[4],[1]])
wr=R.T@w
I20,I30=1/4*m*r**2,1/4*m*r**2
x=array([[wr[0,0]],[wr[1,0]],[wr[2,0]],[I20],[I30]])
for t in arange(0,1,dt):
I2,I3=x[3,0],x[4,0]
I1=I2+I3
I=diag([I1,I2,I3])
wr=array([[x[0,0]],[x[1,0]],[x[2,0]]])
draw_wheel(R,I,wr)
u=array([[0],[0]])
R=R@expw(dt*wr)
x=array([[wr[0,0]],[wr[1,0]],[wr[2,0]],[I2],[I3]])
x=x+dt*f(x+(dt/2)*f(x,u),u)
from sympy import *
from sympy.diffgeom import *
from roblib import * # available at https://www.ensta-bretagne.fr/jaulin/roblib.py
def draw_wheel(R,I,wr,colorwheel="black"):
clean3D(ax,-3,3,-3,3,-1,5)
w=R@wr
L=R@I@wr # angular momentum
draw_arrow3D(ax,0,0,2,0.05*L[0,0],0.05*L[1,0],0.05*L[2,0],"red")
draw_arrow3D(ax,0,0,2,0.3*w[0,0],0.3*w[1,0],0.3*w[2,0],"green") # spin vector
l2,l3=sqrt(abs(I[2,2]-I30+0.5)),sqrt(abs((I[1,1]-I20+0.5)))
M=tran3H(0,0,2)@ToH(R)@wheel3H(r)
draw3H(ax,M,colorwheel,True,1)
def draw_masses(l2,l3,col):
p=array([[0],[0],[2]])+R@array([[0],[l2],[l3]])
ax.scatter(*p,color=col)
draw_masses(l2,0,'green')
draw_masses(-l2,0,'green')
draw_masses(0, l3,'black')
draw_masses(0,-l3,'black')
pause(0.001)
def Symb_build(opt):
init_printing(use_unicode=True) # allow LaTeX printing
w1,w2,w3,I2,I3=symbols("w1 w2 w3 I2 I3")
I20,I30=symbols("I20 I30")
C=CoordSystem('C',Patch('P',Manifold('M',5)),[w1,w2,w3,I2,I3])
w1,w2,w3,I2,I3 = C.coord_functions()
E=C.base_vectors()
F=-((I3-I2)/(I2+I3))*w2*w3*E[0]+-w3*w1*E[1]+w1*w2*E[2]
G1=-(w1/(I2+I3))*E[0]-(w2/I2)*E[1]+E[3]
G2=-(w1/(I2+I3))*E[0]-(w3/I3)*E[2]+E[4]
V0=1/2*(I2-I20)**2 + 1/2*(I3-I30)**2
if opt=="align": V = 1/2*(w2)**2 + 1/2*(w3)**2 + V0
if opt=="passiv": V = 1/2*(I2+I3)*w1**2+ 1/2*I2*w2**2 + 1/2*I3*w3**2 + V0
if opt=="precession": V = 1/2*((I3-I2)*w2*w3)**2 + 1/2*((I2)*w1*w3)**2 + 1/2*((-I3)*w1*w2)**2 + V0
LfV=simplify(LieDerivative(F,V))
Lg1V=simplify(LieDerivative(G1,V))
Lg2V=simplify(LieDerivative(G2,V))
print("L(F,V))=",latex(LfV))
print("L(G1,V))=",latex(Lg1V))
print("L(G2,V))=",latex(Lg2V))
λV=lambdify((w1,w2,w3,I2,I3,I20,I30),V)
λLfV=lambdify((w1,w2,w3,I2,I3,I20,I30),LfV)
λLg1V=lambdify((w1,w2,w3,I2,I3,I20,I30),Lg1V)
λLg2V=lambdify((w1,w2,w3,I2,I3,I20,I30),Lg2V)
return λV,λLfV,λLg1V,λLg2V
def f(x,u):
w1,w2,w3,I2,I3=x[0,0],x[1,0],x[2,0],x[3,0],x[4,0]
I1=I2+I3
u1,u2=u[0,0],u[1,0]
dw1=-((I3-I2)/I1)*w2*w3-w1*(u1+u2)/I1
dw2=-w3*w1-w2*u1/I2
dw3= w1*w2-w3*u2/I3
dI2=u1
dI3=u2
return array([[dw1],[dw2],[dw3],[dI2],[dI3]])
def control(x):
w1,w2,w3,I2,I3=x[0,0],x[1,0],x[2,0],x[3,0],x[4,0]
V1= λV(w1,w2,w3,I2,I3,I20,I30)
Lg1V=λLg1V(w1,w2,w3,I2,I3,I20,I30)
Lg2V=λLg2V(w1,w2,w3,I2,I3,I20,I30)
#LfV = λLfV(w1,w2,w3,I2,I3,I20,I30)
V.append(V1)
u=-(1/sqrt((Lg1V)**2+(Lg2V)**2))*array([[Lg1V],[Lg2V]])
return u
def simu(E,t1,t2,colorwheel="black"):
print("Control strategy : ",E)
global λV,λLfV,λLg1V,λLg2V
λV,λLfV,λLg1V,λLg2V=Symb_build(E)
global R,x
for t in arange(t1,t2,dt):
I2,I3=x[3,0],x[4,0]
I1=I2+I3
I=diag([I1,I2,I3])
II2.append(I2-I20)
II3.append(I3-I30)
wr=array([[x[0,0]],[x[1,0]],[x[2,0]]])
#draw_wheel(R,I,wr,colorwheel)
T.append(t)
W1.append(wr[0,0])
W2.append(wr[1,0])
W3.append(wr[2,0])
Ek.append((0.5*wr.T@I@wr)[0,0])
Ep.append(norm(ad(I@wr)@wr))
u=control(x)
R=R@expw(dt*wr)
x=array([[wr[0,0]],[wr[1,0]],[wr[2,0]],[I2],[I3]])
x=x+dt*f(x+(dt/2)*f(x,u),u)
return
if __name__ == "__main__":
ax= Axes3D(figure())
dt=0.002
r=1
m=10
R=eye(3)
#wr=R.T@w
T,W1,W2,W3=[],[],[],[]
Ek,Ep,Lz,V,Tr,II1,II2,II3=[],[],[],[],[],[],[],[]
I20,I30=1/4*m*r**2,1/4*m*r**2
opt=1 # alignment : the i vector of the well should be aligned with the angular momentum
opt=2 # passivity based control
opt=3 # precession"
opt=4 # allign followed by precession"
if opt==1:
print("\n Aligment control \n ")
x=array([[0.00001],[10],[0],[I20],[I30]])
simu("align",0,40,"red")
if opt==2:
print("\n Passivity control \n ")
x=array([[10],[4],[1],[I20],[I30]])
simu("passiv",0,40,"green")
if opt==3:
print("\n Precession control \n ")
x=array([[10],[4],[1],[I20],[I30]])
simu("precession",0,80,"blue")
if opt==4:
print("\n Alignment controlled followed by a precession control \n ")
x=array([[0.00001],[10],[0],[I20],[I30]])
simu("align",0,20,"red")
simu("precession",20,40,"blue")
print("x=",x)